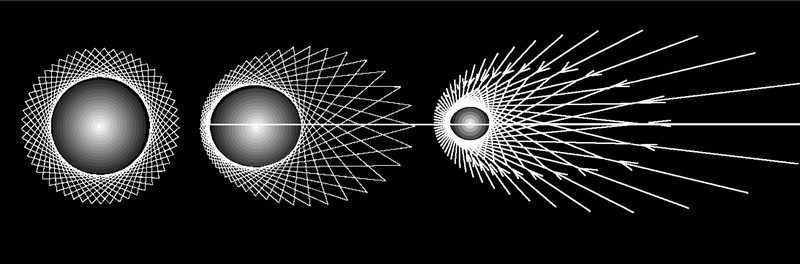
Das schwingende Gleichgewicht und Bohmsche Führungswellen

Im Gleichgewicht zu sein

ist eine ungenaue Bezeichnung, denn Gleichgewichtsprozesse sind durch die Aufeinanderfolge von sehr viel kürzeren Nichtgleichgewichtsprozessen charakterisiert, wobei die jeweils erreichten Grenzzustände um einen dazwischen liegenden Zustand schwingen - dem Gleichgewicht.
Die Materiewelle als Gleichgewichtsprozess angesehen oszilliert mit der Frequenz f um eine mittlere Gestalt. Der harmonische Oszillator der Quantenmechanik (QM) ist demnach eine ´pulsierende´ Schwingungsfigur, wobei deren Ausdehnung im Einzeltfall zyklisch (~f) größer oder kleiner ausfallen kann.  In einer Umgebung mit ausgeglichener Energie- (Impuls-)bilanz, also einem in unserem Sinne idealen Inertialsystem, ist die einfachste Schwingungsgestalt der Materiewelle kugelförmig. Die Summe aller Impulse ergibt  0

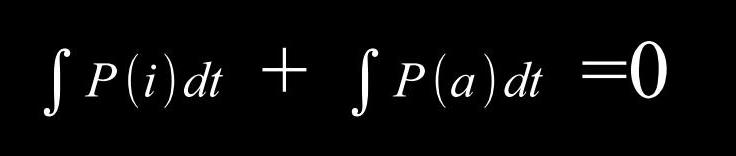
Die Ausgeglichenheit der Impulse über die  ´Oberfläche´ der unten skizzierten Materiwelle ist hier vereinfacht mit Hilfe der Summation der Impulse dargestellt. Die, bezogen auf die Bewegungsrichtung unterschiedliche Dichte der ´Kollisionspunkte´ zwischen Materiewelle und der Umgebung folgt den unterschiedlichen WW- Querschnitten der Materiewelle gegenüber ihrer Umgebung. Auf der ´Anpassungsfähigkeit´ dieser WW-Querschnitte zur Umgebung beruht das Gleichgewicht.

Bei einer Bewegung der Materiewelle gegenüber einer Umgebung mit ausgeglichener Energie- (Impuls-)bilanz, wird ihre Schwingungsgestalt aber von Außen gesehen wegen der Gleichgewichtsbedingung nicht mehr kugelförmig sein können. Sie wird z.B. die unten rechts (in 2D) dargestellten Form annehmen (als statisches Bild).

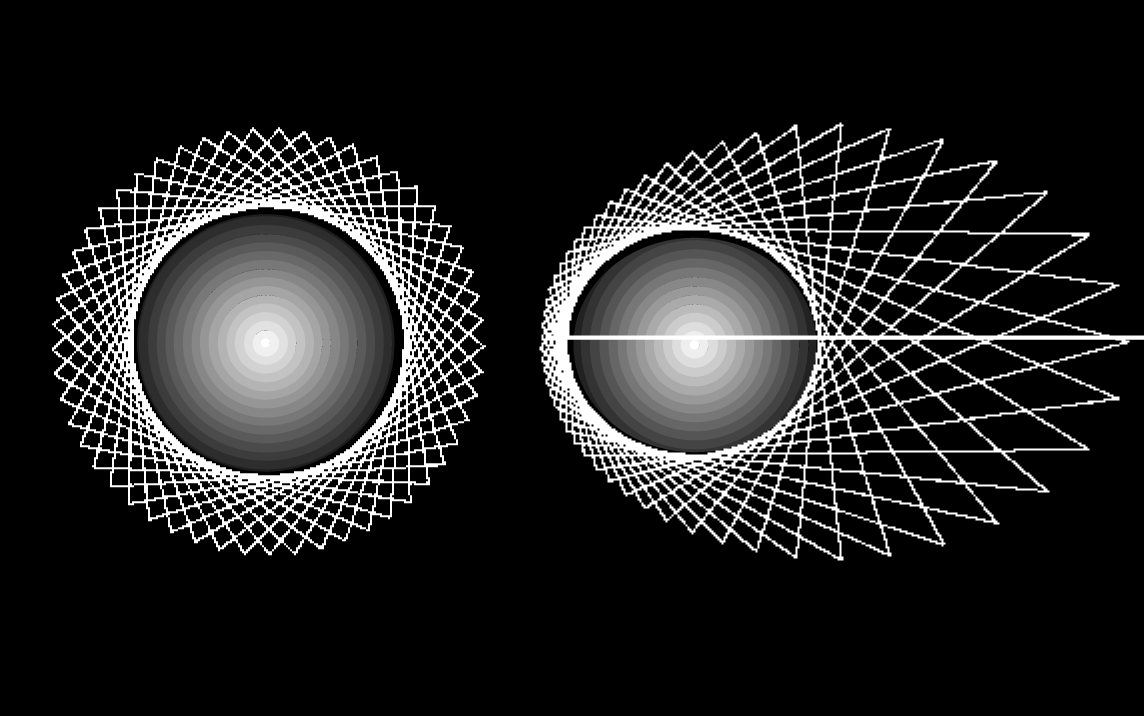
Erläuterung zur Darstellung hier

Die bewegte Materiewelle selbst kann ihre Veränderung aber nicht ´wahrnehmen´. Jede Materiewelle, ob gleichförmig gegenüber dem Ruhsystem bewegt oder nicht, ´fühlt´ sich subjektiv ´rund´. Dies ist eine direkte Folge des Gleichgewichtszustandes zur lokalen Umgebung, wie auch die Erfahrung, dass die Physik in gleichförmig zueinander bewegten Bezugssystemen ununterscheidbar ist  - Invarinaz. Auch eine vormals ruhende, aber infolge einer Beschleunigung bewegte und dadurch veränderte Materiewelle,´fühlt´ sich nach wie vor rund -  aber sie nimmt ihre Umgebung nun anders wahr als vorher.

Die Frequenz des Pulsierens um eine mittlere Gestalt steht für die Eigenfrequenz des Teilchens.

Bei der Herleitung der Lorentztransformation aus der Gleichgewichtsforderung hatte ich z.B. hier die obige bildliche Darstellung der Materiewelle verwendet.  Um aber z.B. anhand des Doppelspaltexperimentes die Effekte der QM darzustellen, ist es m.E. anschaulicher die Materiewelle als eine, um einen Mittelwert pulsierende Kugel darzustellen.

Ob ruhend oder bewegt: die Materiewelle steht in WW zur Umgebung und von ihr aus gehen zyklisch die, infolge der WW leicht veränderten Impulse, wieder in den Raum. Eine zum idealen Inertialsystem bewegte Materiewelle pulsiert ebenso und auch von ihr gehen deshalb ebenso gepulste ´virtuelle´ Wellen in den Raum.
Da sich die Materiewelle immer langsamer bewegt als die virtuellen Wellen, ergibt sich die Situation wie im Bild unten. Die virtuellen Wellen treffen dann natürlich auch auf den Schirm und erfahren vom Zustand des zweiten Spaltes....

Bild unten: Phasen einer  Materiewelle und die von ihr ausgehenden virtuellen Wellenfronten (von links nach rechts im Inertialsystem unterwegs)

Kommen wir zum Doppelspaltversuch:

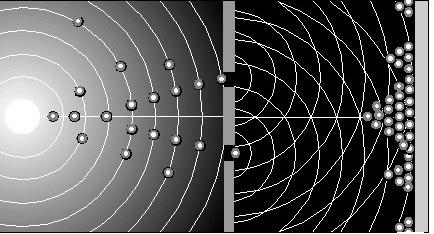
Die Überlagerungsprodukte der blauen virtuellen Wellen im Bild darüber werden auch jenseits des Spaltes ankommen und, da resonant zur Teilchenfrequenz, in dieses hinein kumulieren und damit lenkend auf die Bahn der Materiewelle jenseits des Schirmes einwirken. Bohm nannte sie Führungswellen.

Zur Kausalität der Quantenmechanik:
Nach der oben beschriebenen Interpretation könnten wir zwar gedanklich von einer prinzipiellen Determiniertheit des Geschehens beim Doppelspaltversuch ausgehen, aber wir müssen gleichzeitig anerkennen, dass es uns wegen der WW mit Welthintergrund unmöglich ist, alle an dem Geschehen beteiligten Parameter zu erkennen. Als materielle Beobachter sind diese Einflüsse uns prinzipiell nicht bekannt. Wir können sie nicht einmal  ´beobachten´ ohne sie zu beeinflussen, weshalb jede Prognose immer nur statistischer Natur sein kann.