Dies ist die Physikseite
Elektromagnetische Wechselwirkung
Teil 6 Kreisstrom, Spule und ElektronRückblick
Wir haben hier gesehen, dass sich um einen Leiter immer dann ein Magnetfeld bildet, wenn darin ein Strom fliesst.
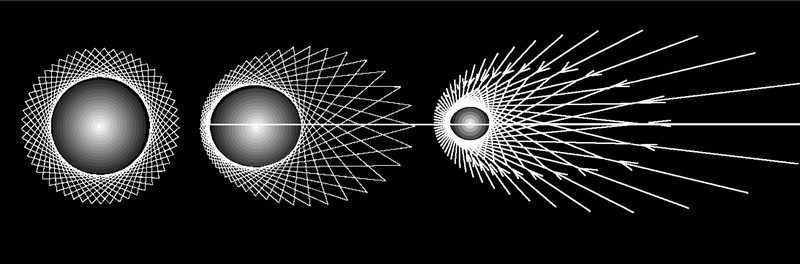
Bild unten: M. Faraday hat die Wirkungen des Magnetfeldes so dargestellt:

Wir haben die magnetische Komponente mit Hilfe von Strömen von ITO dargestellt.
Der Kreisstrom - Elektromagnetische Wechselwirkung
Wenn in einem Leiter Strom fließt, stellen wir uns in der Regel vor, dass Elektronen in eine Richtung fließen. Wenn der Leiter in enem Kreis geschlossen ist, werden die Elektronen also im Kreis fließen.
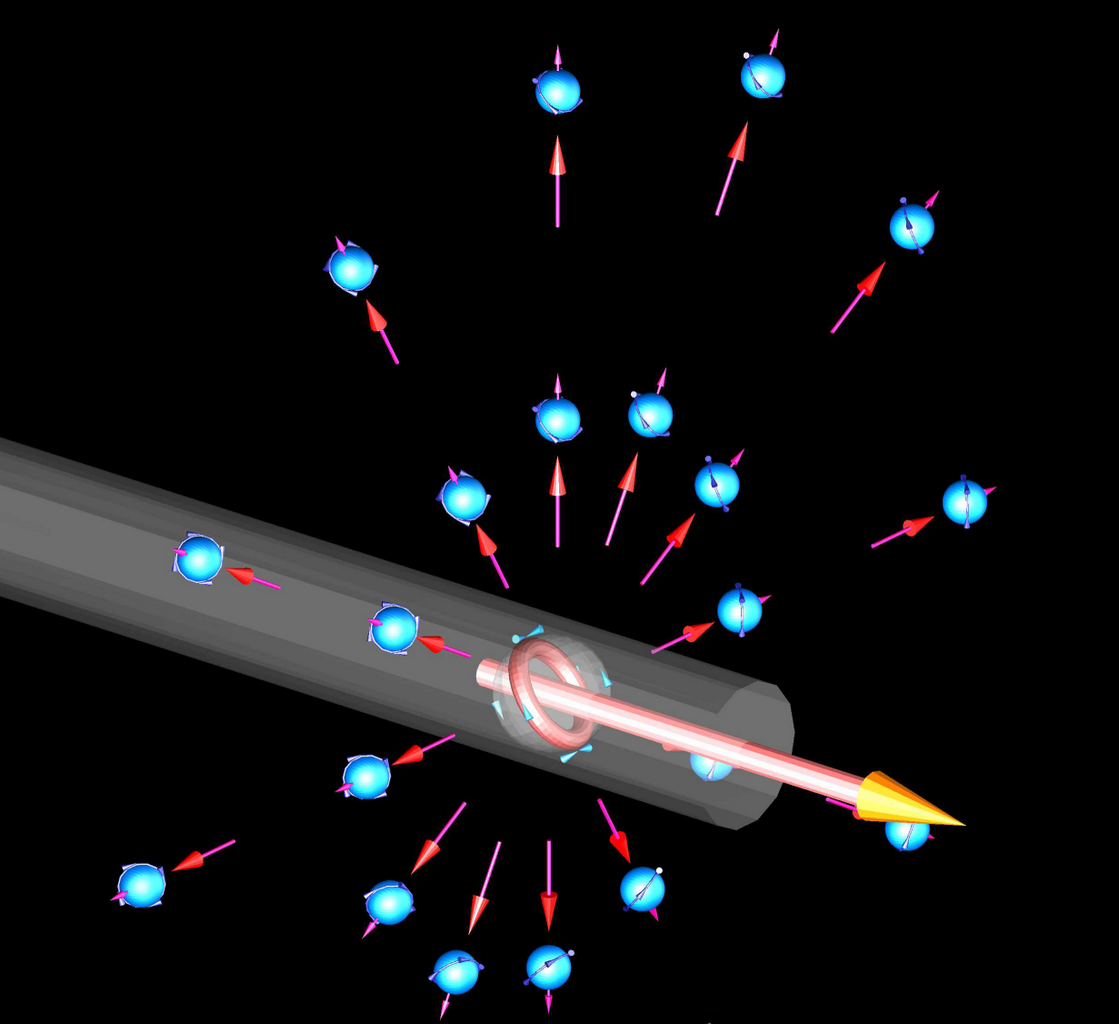
Bild: Im Modell des Kreisstroms gehen vom Leiter in alle Raumrichtungen codierte ITO aus.
Sie tragen jeweils die Codierung der Ladungsquellen: Drehrichtung und Achsneigung entsprechend der Bewegungsgeschwindigkeit
der Quellen.
Im Bild unten sind lediglich die von bewegten Elektronen orthogonalen ausgehenden ITO dargestellt .
Im Bild unten sind lediglich die von bewegten Elektronen orthogonalen ausgehenden ITO dargestellt .

räumlich dargestellt:
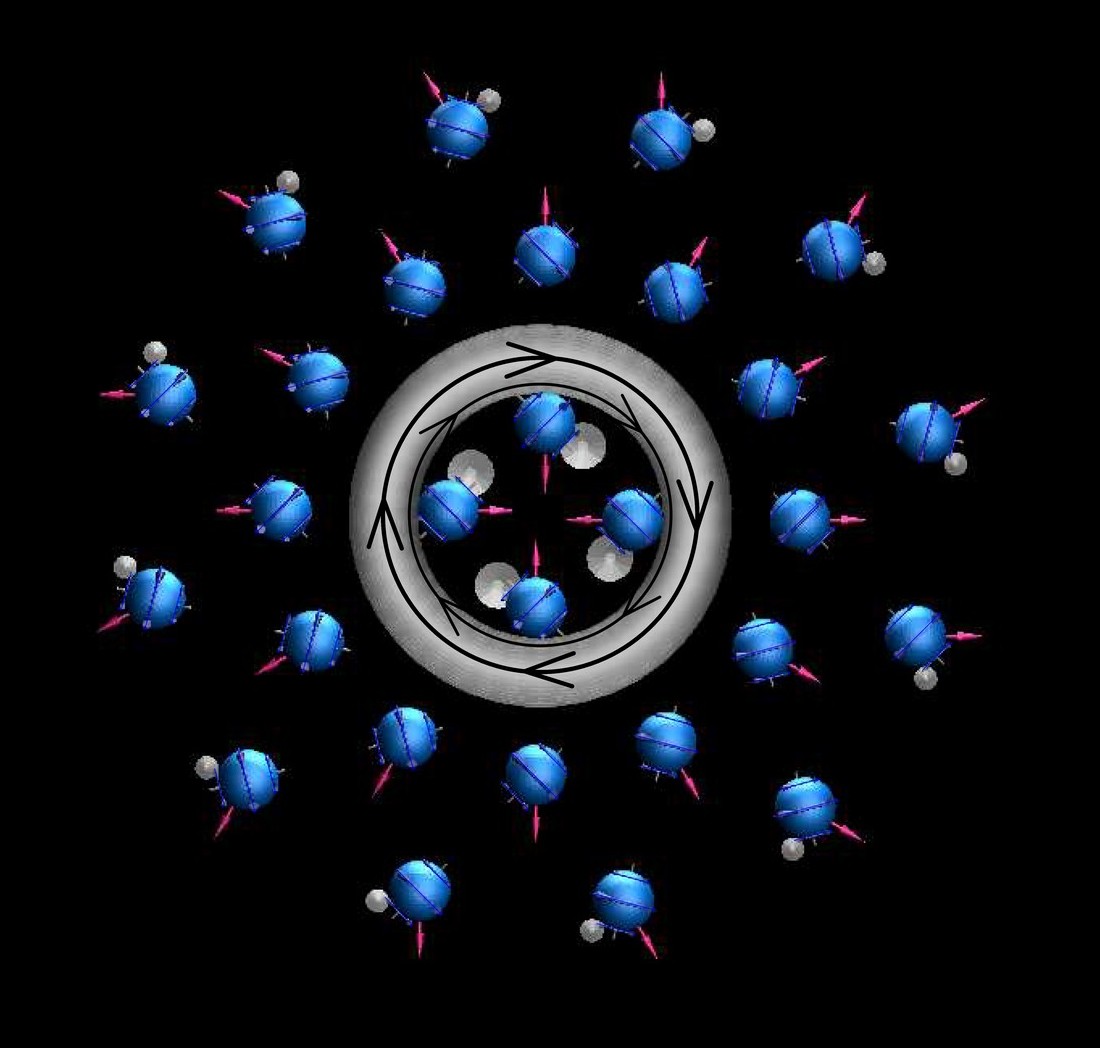
2. Die Bilder oben sind vereinfacht, da die von bewegten positiven Ladungsquellen ausgehenden ITO nicht dargestellt sind. -> Animation unten.

Bild
unten: Eine Momentaufnahme des Kreisstroms zeigt die von den entgegengesetzt bewegten Ladungsquellen
ausgehenden ITO-Ströme
- und die von ihnen im Raum vermittelte magnetische Komponente (grauer Ring, Linke-Hand-Regel).
- und die von ihnen im Raum vermittelte magnetische Komponente (grauer Ring, Linke-Hand-Regel).
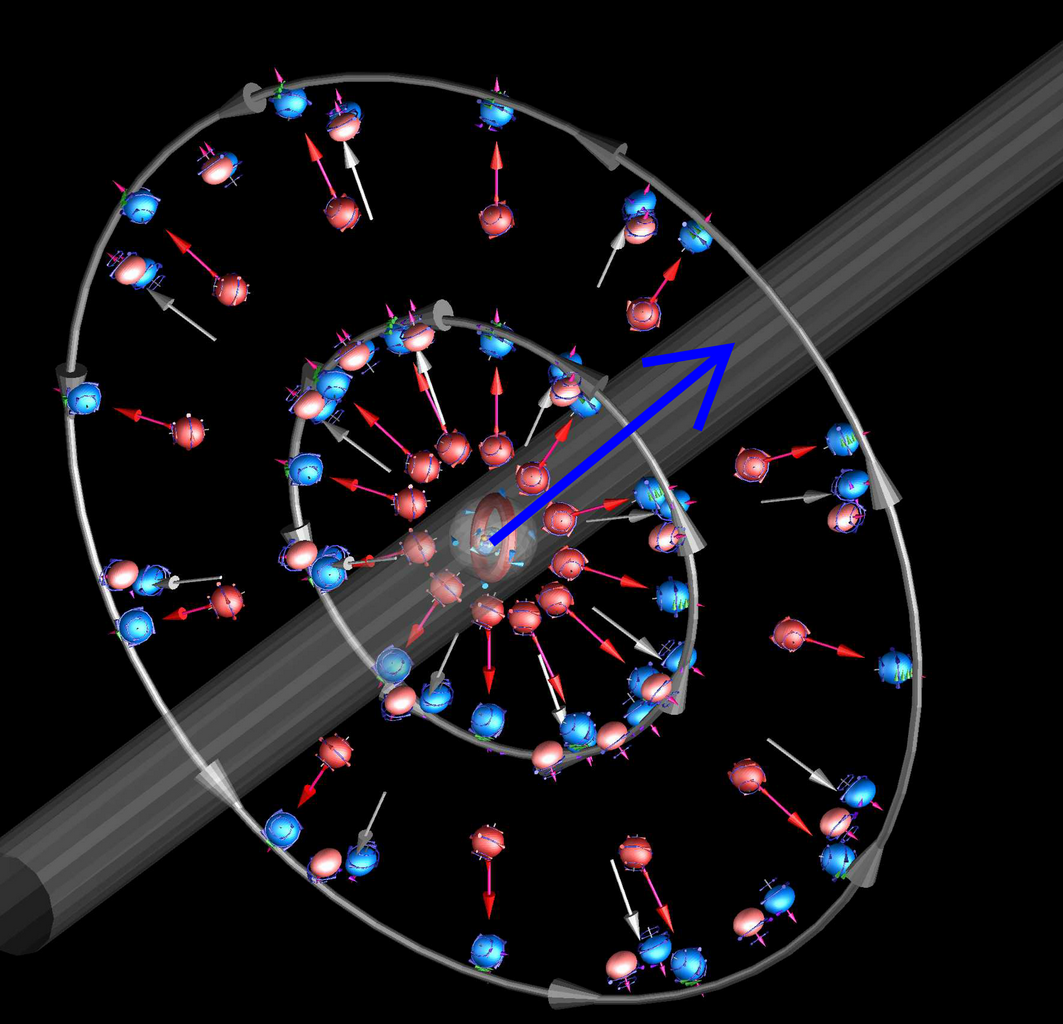
Bild unten: Detail der vom Kreisstrom ausgehenden geprägten ITO - in Momentaufnahme
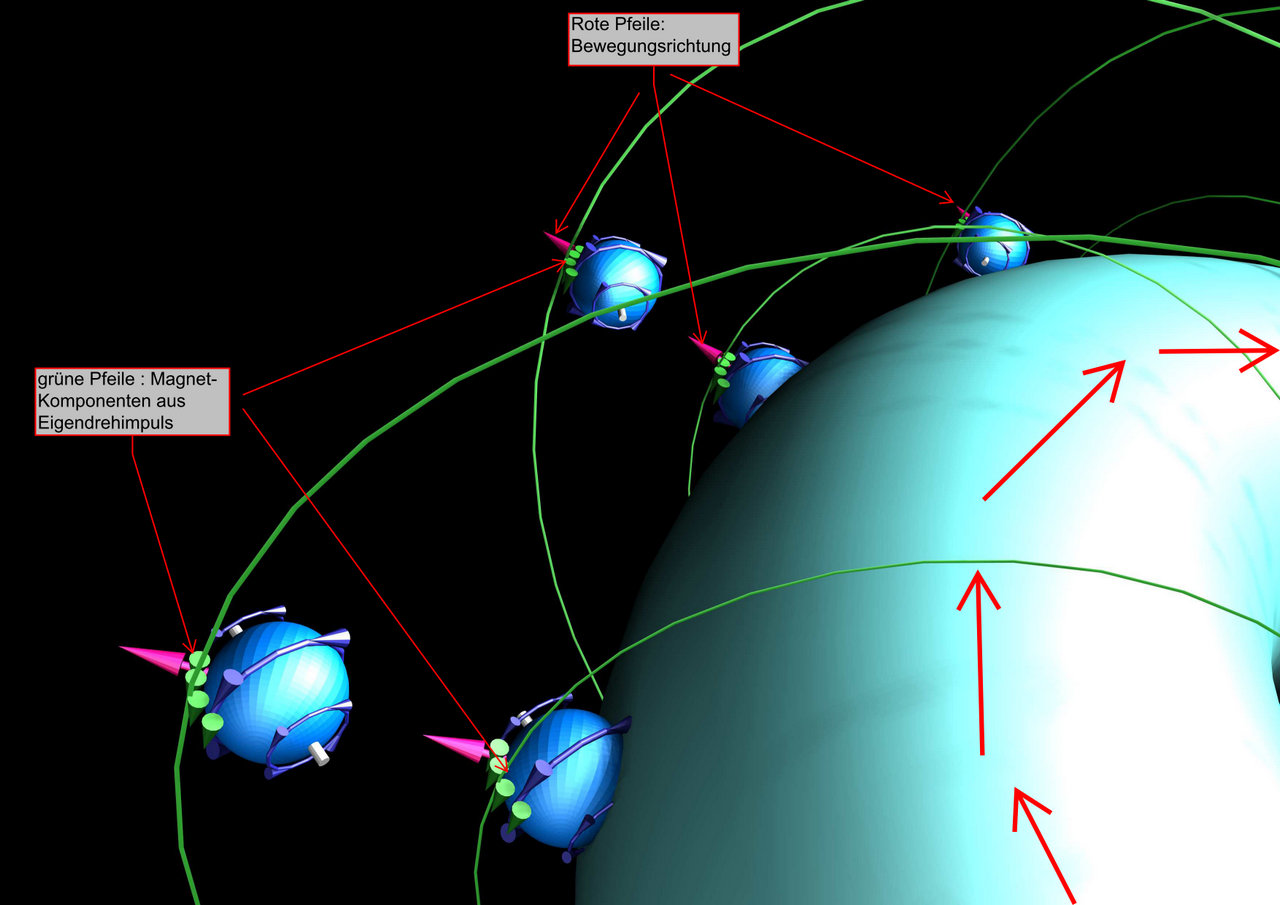
Die im Leiter kreisenden Elektronen und Defektelektronen bilden das Feld. Hintergrund-ITO hier nicht dargestellt
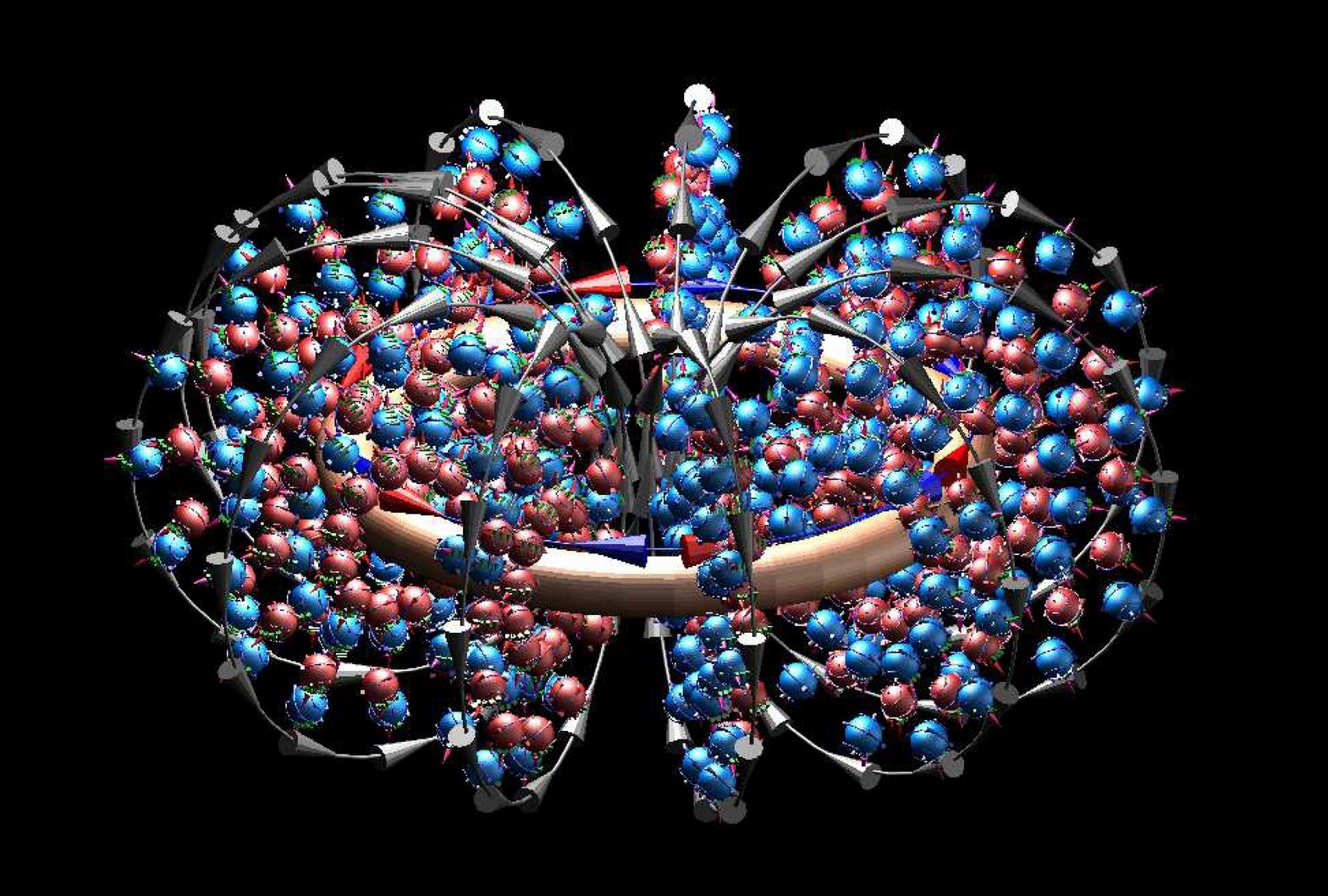
Legt man viele Leiterkreise
übereinander, lässt darin einen Strom in die gleiche Richtuing fießen,
dann ziehen die Leiter einander an (Lorentzkraft)
und die Ströme der von ihnen ausgehenden ITO -der von ihnen ausgehende
Fluss- überlagern sich. Beispiele dafür finden wir z.B. in einer Spule
oder im Permanentmagnet.
Bild unten: gleich gerichtete Kreisströme übereinander. Die magenetische Komponenten überlagern sich.
Es sind nur die zum Leiter orthogonalen ITO Ströme dargestellt)
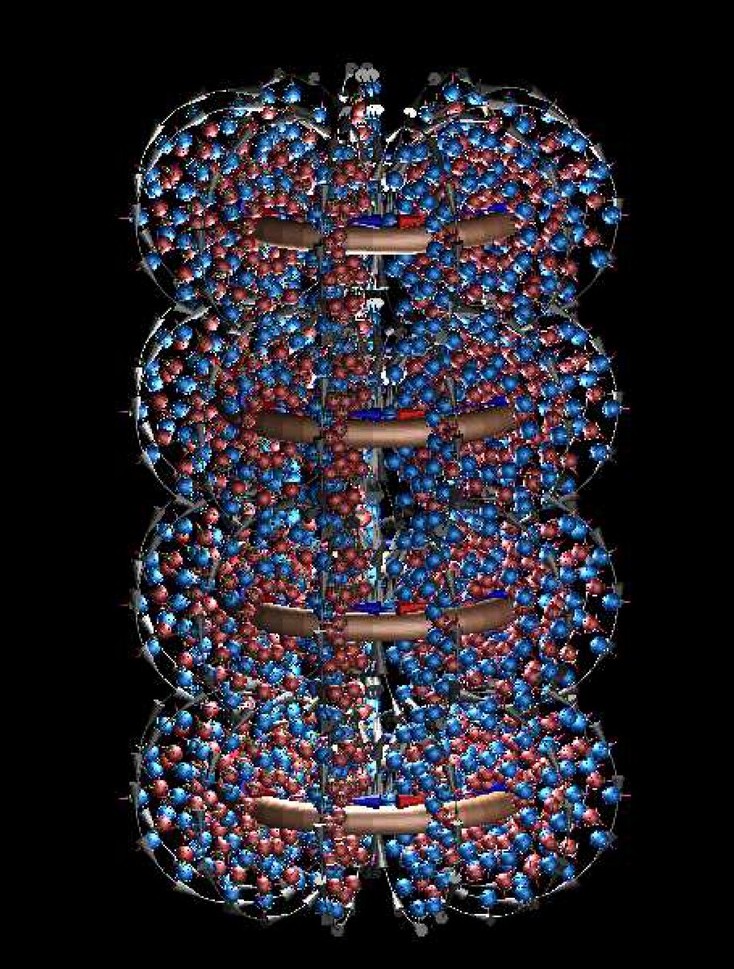
Bild unten: Viele Kreisströme ´untereinander´ - die Überlagerung der ITO Ströme führt zur Ausbildung des Feldes, das mit Feldlinien dargestellt wird.
Dieses Feld wirkt auf geeignete (magnetische) Partikel, welche in den vom Fluss durchdrungenen Raum eindringen, zu sehen z.B. hier
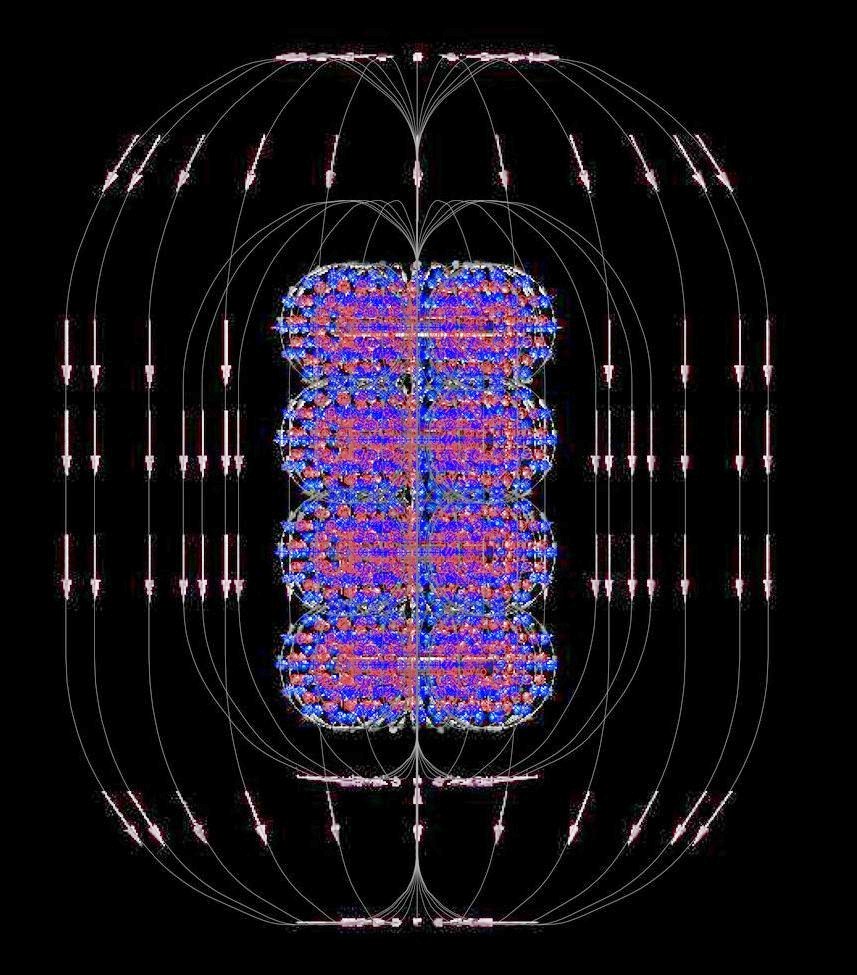
In einer stromdurchflossenen Spule überlagern sich die Felder der einzelnen Windungen. Es ergibt sich ein Feldlinienverlauf wie von Faraday beschrieben.
Das Magnetfeld von Permanentmagneten
Es beruht auf speziellen Eigenschaften des ferromagnetischen Materials, bei dem um den Atomkern schwingende Elektronen einen Mikrokreisstrom bilden. Sind die Schwingebenen der Valenzelektronen der Atome gleich gerichtet, dann bewirken diese Mikrokreisströmen ebenso ein Magnetfeld.
Siehe auch hier: Magnetismus von Festkörpern Es beruht auf speziellen Eigenschaften des ferromagnetischen Materials, bei dem um den Atomkern schwingende Elektronen einen Mikrokreisstrom bilden. Sind die Schwingebenen der Valenzelektronen der Atome gleich gerichtet, dann bewirken diese Mikrokreisströmen ebenso ein Magnetfeld.
Bild unten:
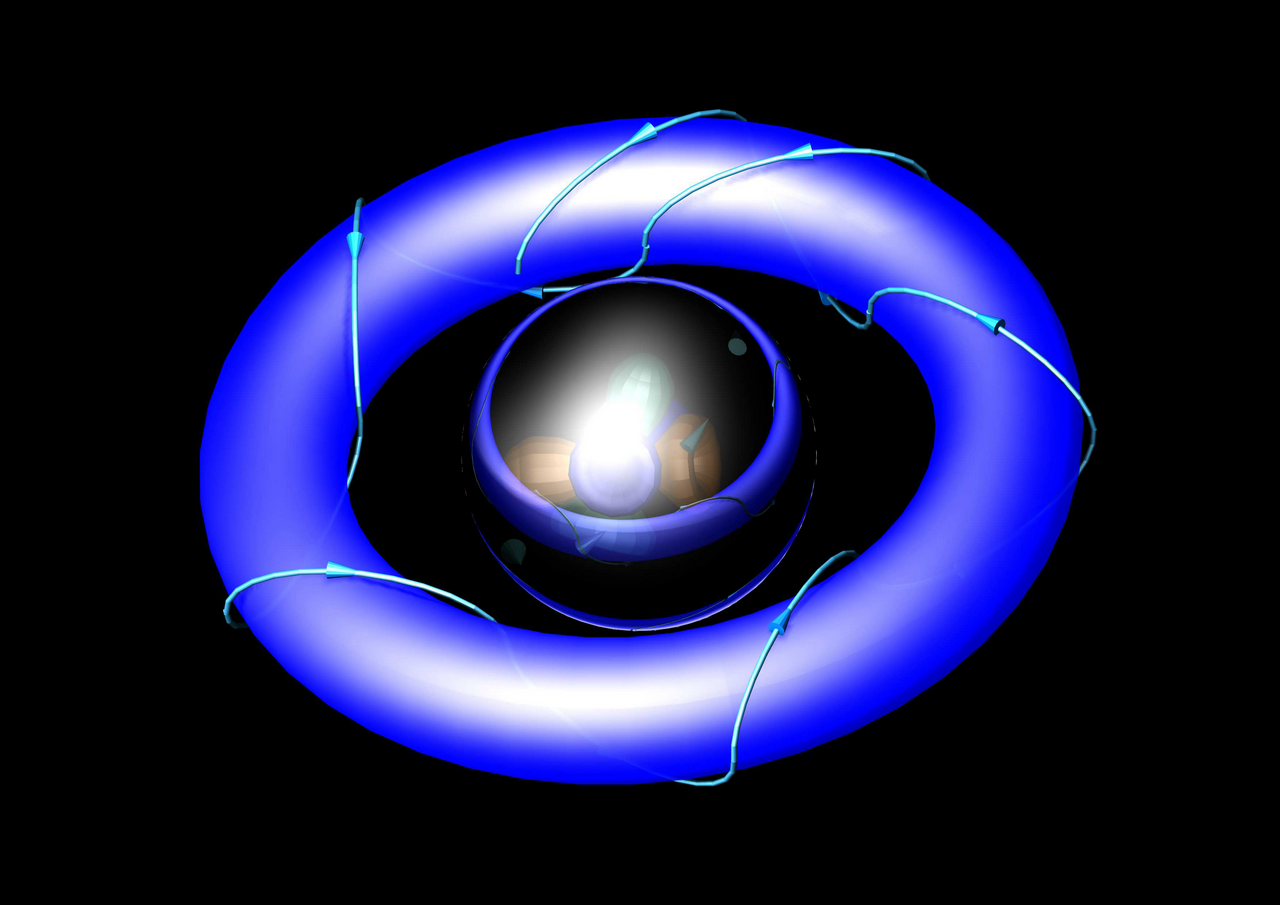
Die (vereinfachte) Schwingungsfigur des Elektrons eines H-Atoms. Das Elektron, oder genauer gesagt die Energie des Elektrons ist im Areal des Torus um den Kern zu finden.
Die Bilder zeigen das gleiche Atom - eiknmal ´von oben´ und einmal ´von unten´.

Die (vereinfachte) Schwingungsfigur des Elektrons eines H-Atoms. Das Elektron, oder genauer gesagt die Energie des Elektrons ist im Areal des Torus um den Kern zu finden.
Die Bilder zeigen das gleiche Atom - eiknmal ´von oben´ und einmal ´von unten´.


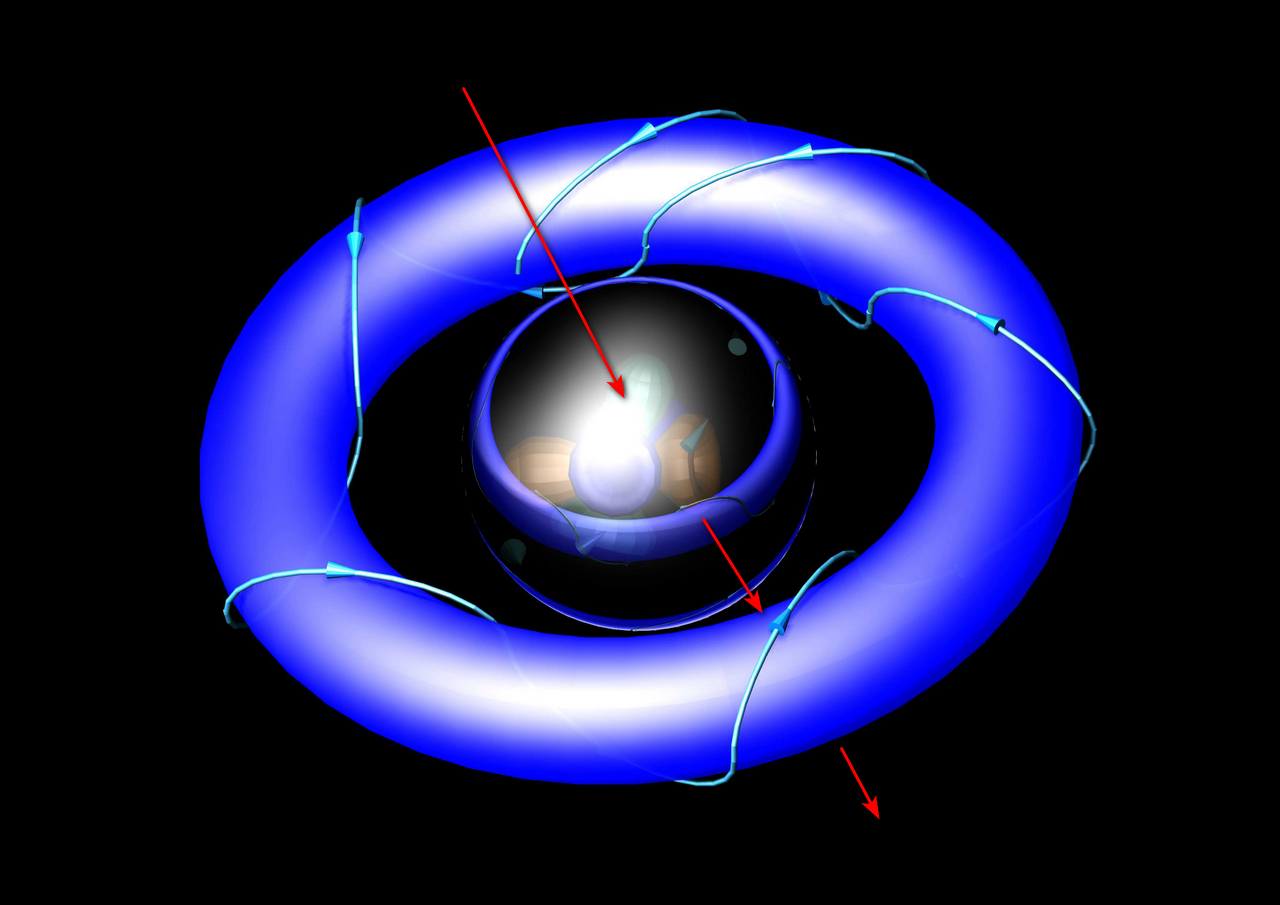
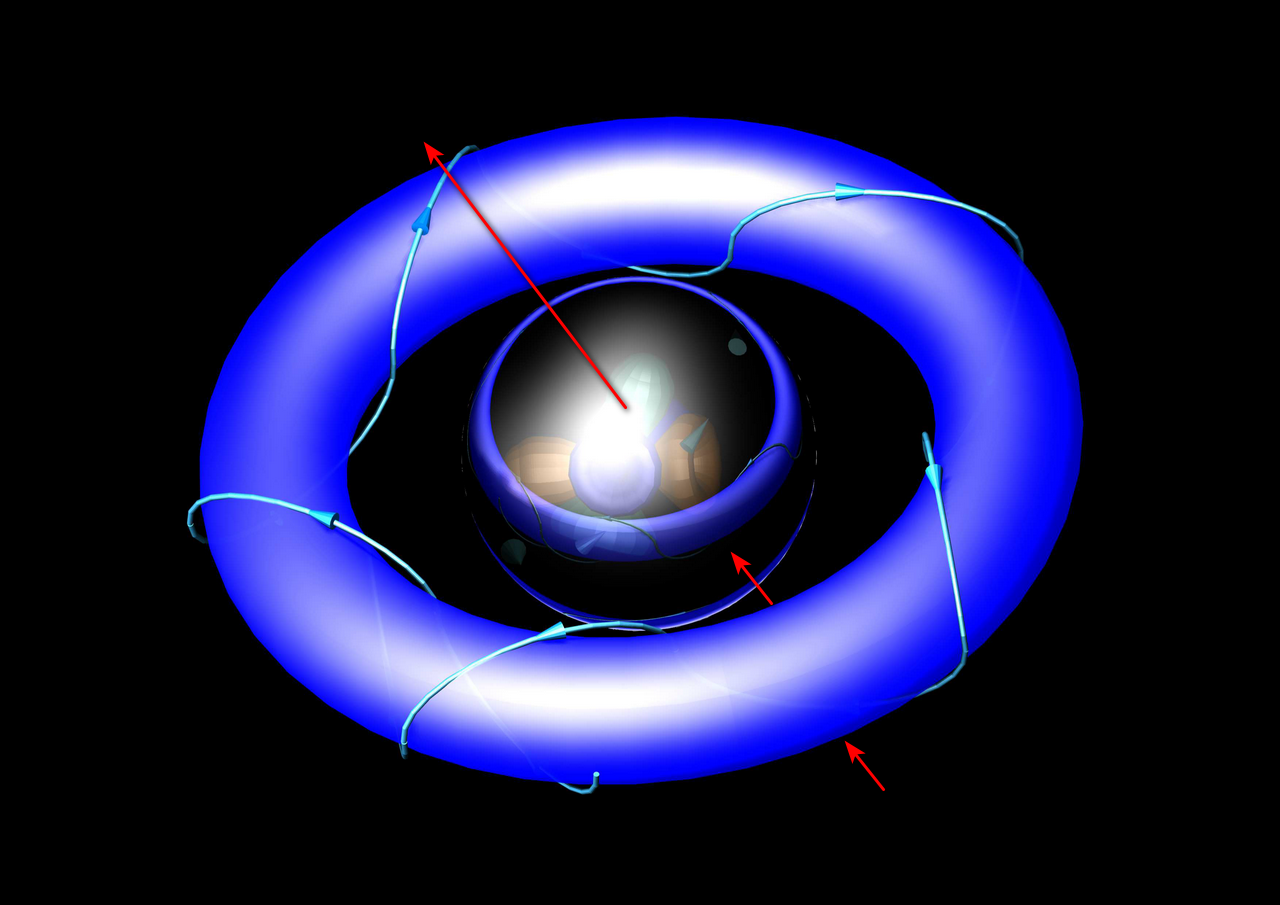
Bilder H-Atom mit einfachen Tori und der magnetischen Einstellung - von unten und oben.
Hinweis: Zweifache Spiegelung führt zum Ausgangszustand!
Die Linien um den Torus veranschaulichen die zyklische WW- Spur des e- mit den Hintergrund- ITO und den ITO vom Atomkern. Die Richtung der WW-Spur definiert die Richtung des Stroms und damit - weil es ein Kreisstrom ist - die Richtung des magnetischen Moments des e- des Atoms.
Das Elektron (oder Positron) selbst besitzt ein magnetisches Moment!
Dieser Umstand irritiert im ersten Augenblick, da wir bisher in einem Elektron selbst keinen Kreisstrom vermutet hätten. Doch dieser Effekt ist messbar und wird auch längst im Alltag benutzt - zum Beispiel im MRT (da sind es zwar Positronen, aber das sind nur Elektronen mit positiver Ladung).
Wie sollte eine Schwingungsfigur des Elektrons aussehen, damit wir darin einen Kreisstrom erkennen und das magnetischen Moments des Elektrons (oder Positrons) ´ensteht´.
Bild 2 - einfacher Torus mit Magnetpfeil, aber nun nicht als Atom, sondern als zwei einzelne Elektronen
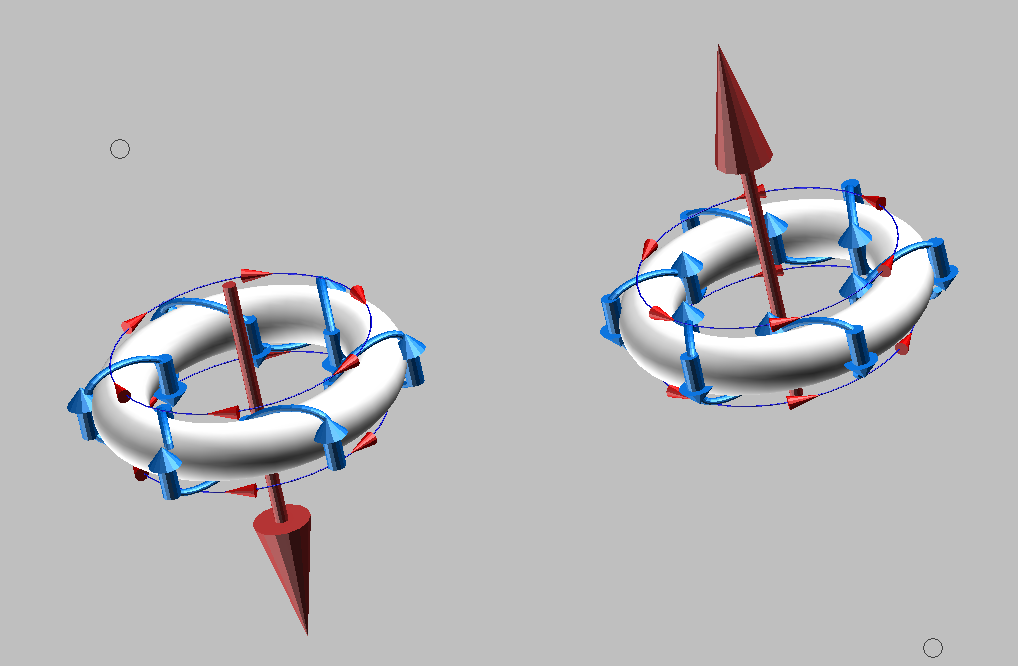
und nun die beiden von unten
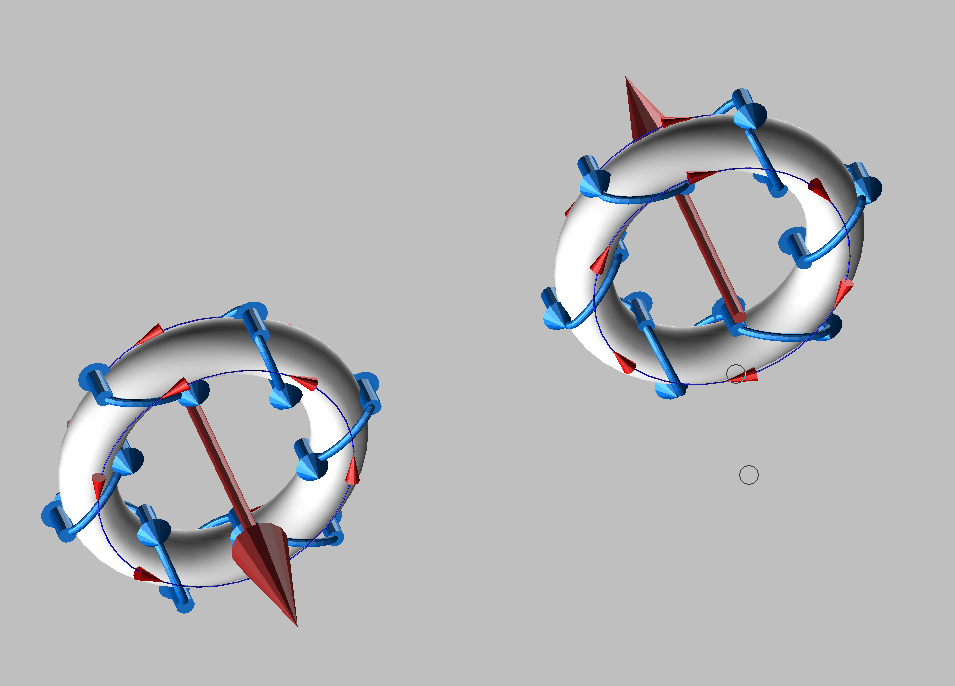
Die Richtung des Kreisstroms definiert die Ausrichtung des Magnetfeldes.
Das Problem beim Elektron:
Das oben skizzierte Kreisstrom-Bild eines Elektrons ist leider zu einfach. Die Wirklichkeit ist komplizierter. Die Quantenmechanik hat die innere Dynamik des Elektrons - den Spin- mathematisch gelöst, aber leider keine anschauliches Bild dazu.
Im QM- Modell kann man das Elektron 180° ´drehen (spiegeln), aber wenn man es nochmal 180° dreht (zurückspiegelt), kommt man nicht wieder beim Ausgangszustand an. Die QM fordert es 4*180° , also 720° zu drehen, ansonsten kommt man nicht wieder in den Ausgangszustand.
Das Modelle oben liefert aber nach 2x180°= 360°, also nach dem einfachen ´zurück spiegeln´, wieder den Ausgangszustand. Es passt also noch nicht ganz. Mehr dazu hier.
Seltsame Attraktoren
Unsere Darstellung oben benutzt zur Veranschaulichung der Stromrichtung um den Kern eine sich um den Torus windende Spirale. Diese Dynamik erinnert an den seltsamen Attraktor, eine stabilen Schwingungsgestalt in einer chaotischen Umgebung.
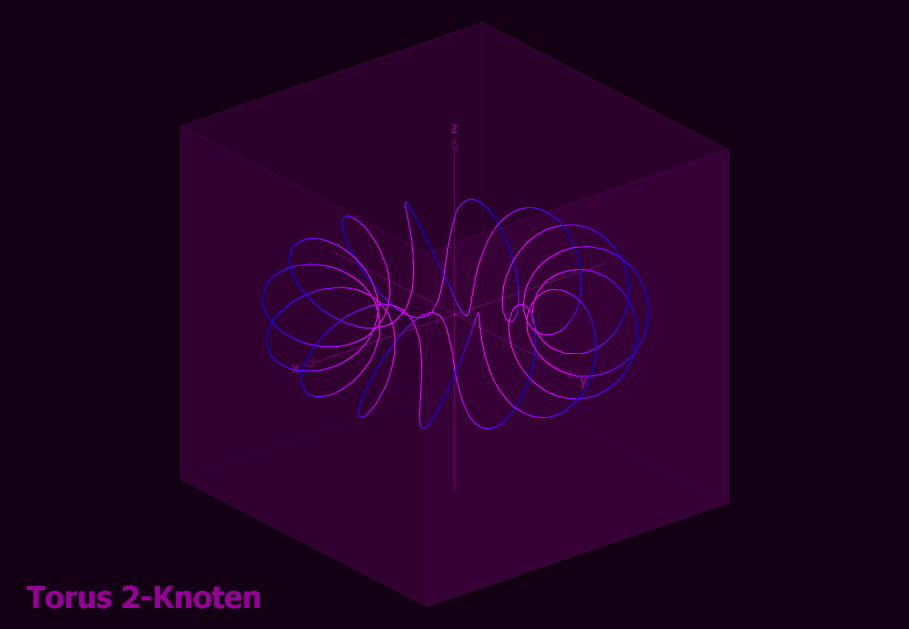
Bild und mehr Info dazu hier Grenzzykelattraktor